Everything about Resnet

Deep Residual Learning for Image Recognition

Jun 13, 2024 13 min read

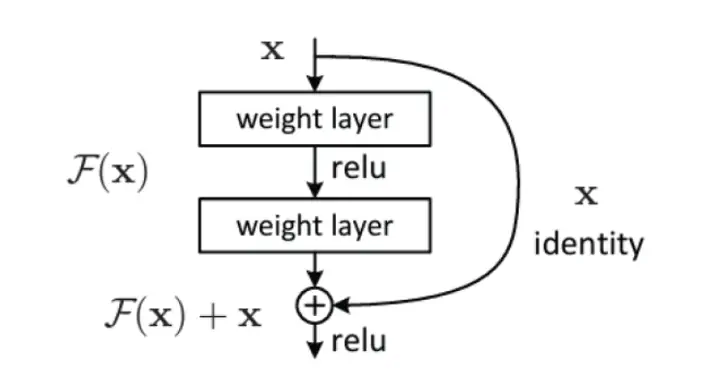Resnet

Deeper networks can capture more complex features and improve performance on challenging datasets like ImageNet. However, increasing the depth of these networks introduces significant challenges, such as vanishing and exploding gradients, which hamper training.

Resnet, or Residual Network, was introduced to address these challenges, particularly the degradation problem observed in very deep networks. The degradation problem refers to the phenomenon where, as the network depth increases, the training accuracy degrades after reaching a certain point, not due to overfitting but because of optimization difficulties.

The core innovation of Resnet lies in its residual learning framework. Instead of learning a direct mapping from input to output, Resnet focuses on learning residuals. Formally, if the desired mapping is H(x), Resnet aims to learn the residual mapping F(x) = H(x) − x. Thus, the network essentially learns H(x) = F(x) + x.

F(x) represents the residual function that the network learns, and the final output is H(x) = F(x) + x

This is achieved through shortcut connections, also known as skip connections, which bypass one or more layers. These shortcut connections perform identity mapping, meaning the input is directly added to the output of the stacked layers. This design makes it easier for the network to learn identity mappings if needed, facilitating the training of very deep networks.

Key Takeaways from the Paper

Resnet stands for residual neural networks and it is a type of [[Convolutional Neural Networks]].
Resolves the problem of [[Vanishing and Exploding Gradients]] in very deep neural networks
Provides us with Deep Resnet that use Residual Connections.
Residual Connections: Resnet incorporates residual connections, which allow for training very deep neural networks and alleviate the vanishing gradient problem.
Identity Mapping or skip connections: Resnet uses identity mapping as the residual function, which makes the training process easier by learning the residual mapping rather than the actual mapping.

Why Resnet? Problem with Old Deep learning Architectures?

Increasing Depth: So, Basically the more the number of neural layers, the more accurate the prediction is.
Degradation Problem: But when we go for very deep neural networks, then the accuracy of the model saturates or decreases instead of increasing, i.e. the training and testing error increases. This degradation is not due to [[overfitting]] , but due to the [[Vanishing and Exploding Gradients]] problem.
- When deeper networks are able to start converging, a degradation problem has been exposed: with the network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. This is the degradation problem, where as you make deep neural networks, they become harder to train. The accuracy might plateau or even degrade as you add more layers.
Intermediate Solutions: The paper mentions that vanishing gradients have been addressed by adding the intermediate normalization layers (see [[Batch Normalization]] ) and normalized initialization.
- This problem, however, has been largely addressed by normalized initialization [23, 8, 36, 12] and intermediate normalization layers [16], which enable networks with tens of layers to start con verging for stochastic gradient descent (SGD) with back propagation.
Additionally In this paper, they address the degradation problem by introducing a deep residual learning framework.

So, How to resolve this problem?

Adding more layers to a suitably deep model leads to higher training errors. ❌
The paper presents how architectural changes like residual learning tackle this degradation problem using residual networks.
Residual Network adds an identity mapping between the layers. Applying identity mapping to the input will give the output the same as the input. The skip connections directly pass the input to the output, effectively allowing the network to learn an identity function.

H(x) = F(x) + x

where, X is the input to the set of layers, F(x) is the residual function, H(x) is the mapping function from input to output.

Instead of trying to directly learn the underlying mapping from input to output (H(x)), Resnet introduces the idea of learning a residual mapping (F(x)).
F(x) represents the difference between the desired output (H(x)) and the input (x). So, instead of trying to learn H(x) directly, the network learns to predict the difference between the desired output and the input.
The hypothesis is that it’s easier to optimize the residual mapping than to optimize the original mapping directly. Essentially, it’s easier for the network to learn how to adjust the input rather than learning the entire mapping from scratch.
Shortcut/Skip Connections: These are direct connections between layers that skip one or more layers in between. In Resnet, these shortcut connections perform identity mapping, meaning they simply pass the input through to the next layer unchanged.
In essence, Resnet tackles the degradation problem in deep neural networks by introducing residual learning, where the network learns to predict the difference between the desired output and the input, making it easier to train very deep networks effectively.

Just learn the residual instead of learning everything.

Here’s how it works in simple terms

Building Blocks : Resnet is made up of many smaller blocks called “residual blocks”. Each block contains a few layers of neural networks.
Shortcut Connections: These blocks have a special feature called “shortcut connections” or “skip connections.” These connections let the information skip one or more layers and jump directly to a deeper layer in the network.
Learning Residuals: Instead of trying to directly learn how to map inputs to outputs, Resnet learns to predict the difference or “residual” between the actual output and the desired output. This makes learning easier because the network only needs to focus on small changes, or adjustments, to the input data rather than trying to learn the entire mapping.
Deeper Networks: Because of these shortcut connections, Resnet can be made much deeper than traditional neural networks without running into problems like vanishing gradients, where the signal gets weaker as it passes through many layers.
Better Performance: By using these shortcut connections and learning residual functions, Resnet can achieve better accuracy and performance compared to other neural network architectures, especially when dealing with very deep networks.

so is it like supervised learning where the model tries to learn the error or difference between the actual data and predicted data?
- In the case of Resnet, it also learns from labeled examples, but instead of directly predicting the output, it learns to predict the difference (residual) between the actual output and the desired output. By focusing on learning these residuals, Resnet can make smaller adjustments to the input data, which can make training easier and more effective, especially in very deep networks.
and the goal is to minimize the residual?
- Exactly! In Resnet, the goal is to minimize the residual, which represents the difference between the actual output and the desired output. By minimizing this residual, the model aims to make its predictions as close to the true labels as possible. This process of minimizing the residual helps the model learn and improve its performance on the task it’s trained for, such as image recognition or object detection.
then how does it resolve the issue of vanishing gradients?
- Through the use of shortcut connections, also known as skip connections or identity mapping.
- so we add the original input value to the whatever output of residual layers we get, so that we don’t lose the gradient?
  - Yeah. In Resnet, the input to a residual block is added to the output of the block, which is then passed through a non-linear activation function (usually ReLU). This addition operation creates a shortcut connection, also known as a skip connection or identity mapping.
  - By adding the original input to the output, the gradient flowing through the network during backpropagation is preserved. Even if the gradient becomes very small in the layers of the residual block, it can still flow through the shortcut connection directly to deeper layers without being significantly affected.

The Resnet block with Code

Let’s look at the code of the Resnet to make the concepts more clear.

if in doubt, code it out.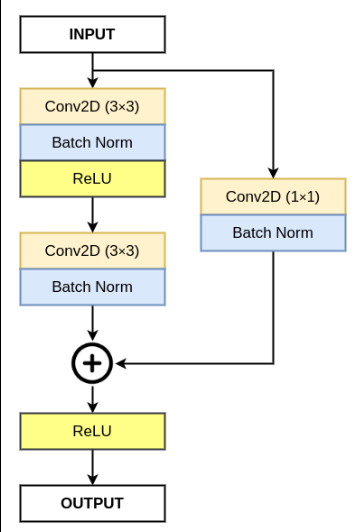

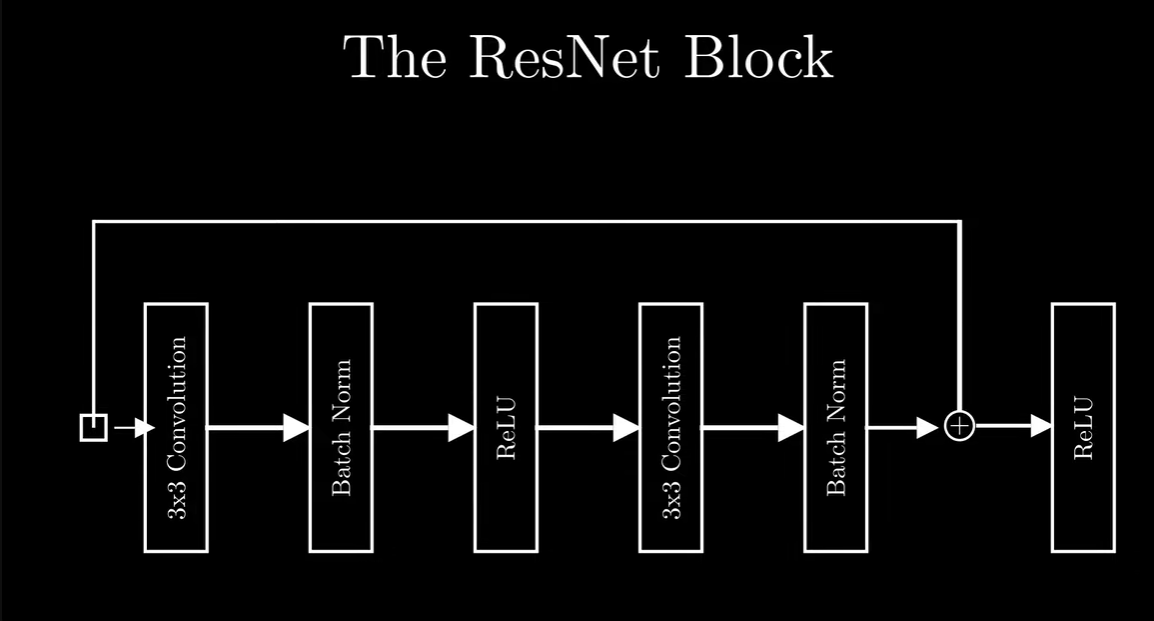
class ResidualBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride = 1, downsample = None):
        super(ResidualBlock, self).__init__()
        self.conv1 = nn.Sequential(
                        nn.Conv2d(in_channels, out_channels, kernel_size = 3, stride = stride, padding = 1),
                        nn.BatchNorm2d(out_channels),
                        nn.ReLU())
        self.conv2 = nn.Sequential(
                        nn.Conv2d(out_channels, out_channels, kernel_size = 3, stride = 1, padding = 1),
                        nn.BatchNorm2d(out_channels))
        self.downsample = downsample
        self.relu = nn.ReLU()
        self.out_channels = out_channels
        
    def forward(self, x):
        residual = x
        out = self.conv1(x)
        out = self.conv2(out)
        if self.downsample:
            residual = self.downsample(x)
        out += residual
        out = self.relu(out)
        return out

Downsample is a parameter for the skip connection because we are summing the original image with the output of conv layers which might have its dimensions reduced. So, to make the dimensions of both same for summing operation , we need to Downsample the initial image.

The convolutional layers mostly have 3 x 3 filters and follow two simple design rules: (i) for the same output feature map size, the layers have the same number of filters; and (ii) if the feature map size is halved, the number of filters is doubled so as to preserve the time complexity per layer.

Consistent Number of Filters: For convolutional layers that produce feature maps of the same size, they typically have the same number of filters. This helps maintain consistency in the information processing across different layers.
Doubling Filters with Halved Feature Map Size: When the spatial dimensions of the feature maps are halved (e.g., through operations like max pooling or convolution with a stride of 2), the number of filters in the subsequent convolutional layer is usually doubled. This increase in filters helps to maintain the computational complexity per layer approximately constant despite the reduction in spatial dimensions.

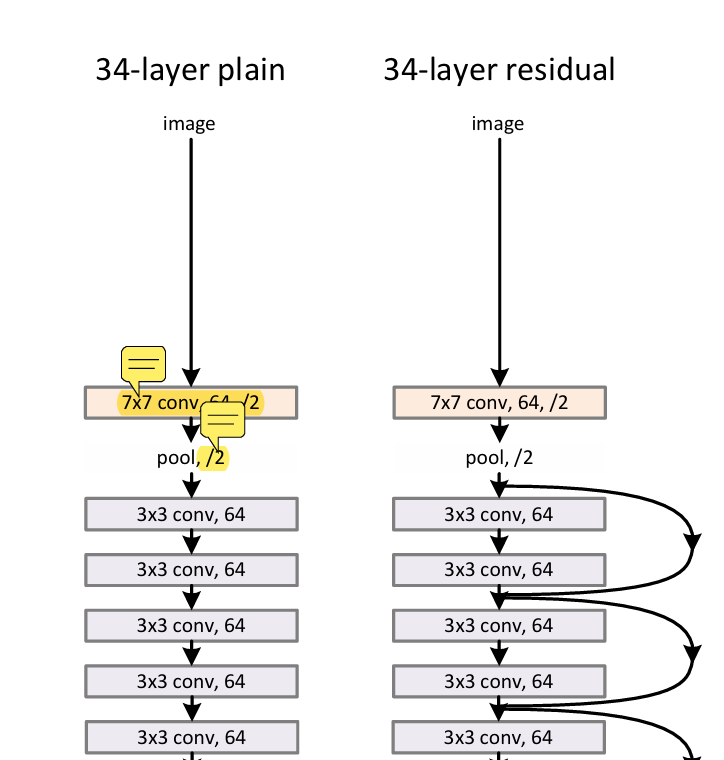
The image provided will be 3x224x224 so the first 7x7 conv layer will get 224 size image and it should reduce to 64 output size right? - yes that’s right. - Output Size: 64x112x112 (64 channels, 112 height, 112 width) - number of feature maps will increase from 3 to 64 according to design rule 2. - So, after the 7x7 convolutional layer with a stride of 2 and padding of 3, the size of the feature map is indeed reduced from 224x224 to 112x112, but the number of channels increases to 64. - How to know how many feature maps will be created then? - In the Resnet architecture you provided, the first convolutional layer (nn.Conv2d) has 64 output channels specified. Therefore, after applying this convolutional layer to the input image of size 224x224, the output will be a feature map with dimensions 64x112x112.

import torch
import torch.nn as nn

device = "cuda" if torch.cuda.is_available() else "cpu"
device

The downsample parameter is used to adjust the number of channels when transitioning between layers in the Resnet architecture.

class ResidualBlock34(nn.Module):
  # In a residual block ,
  # kernel size = fixed 3x3 for all layers
  # input shape  = varies
  # output shape = varies
  # stride  = varies
  # padding = fixed 1
  def __init__(self, in_channels:int, out_channels:int, stride:int , downsample = None):
    super().__init__()
    self.conv1 = nn.Sequential(
        nn.Conv2d(in_channels,out_channels, kernel_size = 3, stride = stride, padding = 1 ),
        nn.BatchNorm2d(out_channels),
        nn.ReLU()
    )
    self.conv2 = nn.Sequential(
        nn.Conv2d(out_channels, out_channels, kernel_size = 3, stride = 1, padding = 1 ),
        # stride should be 1 here cause input and output shape is same so need to match them
        nn.BatchNorm2d(out_channels),
    )
    self.relu = nn.ReLU()
    self.downsample = downsample

  def forward(self, x):
    original = x
    x = self.conv1(x)
    x = self.conv2(x)
    if self.downsample: # needed if the original image shape is not same as the output obtained from the conv layers
      original = self.downsample(original)
    x += original
    x = self.relu(x)
    return x

In Resnet-34,total layer = 4 and in each layer there is [3,4,6,3] Resnet blocks
In Resnet-50,total layer = 4 and in each layer there is [3,4,6,3] Resnet blocks
In Resnet-101,total layer = 4 and in each layer there is [3,4,23,3] Resnet blocks
In Resnet-152,total layer = 4 and in each layer there is [3,8,36,3] Resnet blocks

class Resnet34(nn.Module):
    def __init__(self, ResidualBlock34,layers,  num_classes):
        super(Resnet34,self).__init__()
        self.in_channels = 64
        self.conv1 = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3),
            nn.BatchNorm2d(64),
            nn.ReLU()
        )
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        self.layer0 = self.create_layer(ResidualBlock34, 64, layers[0], stride=1)
        self.layer1 = self.create_layer(ResidualBlock34, 128, layers[1], stride=2)
        self.layer2 = self.create_layer(ResidualBlock34, 256, layers[2], stride=2)
        self.layer3 = self.create_layer(ResidualBlock34, 512, layers[3], stride=2)
        self.avgpool = nn.AdaptiveAvgPool2d(output_size=(1, 1))
        self.fc = nn.Linear(512, num_classes)
        

    def create_layer(self, ResidualBlock34, out_channels, num_blocks, stride):
        downsample = None
        if stride != 1 or self.in_channels != out_channels:
            downsample = nn.Sequential(
                nn.Conv2d(self.in_channels, out_channels, kernel_size=1, stride=stride),
                nn.BatchNorm2d(out_channels),
            )

        all_blocks = []
        all_blocks.append(ResidualBlock34(self.in_channels, out_channels, stride, downsample))
        self.in_channels = out_channels
        # print(self.in_channels)
        for i in range(num_blocks - 1):
            all_blocks.append(ResidualBlock34(self.in_channels, out_channels, 1 , downsample = None))

        return nn.Sequential(*all_blocks)
    

    def forward(self, x):
        x = self.conv1(x)
        x = self.maxpool(x)
        x = self.layer0(x)
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        x = self.avgpool(x)
        x = torch.flatten(x, 1)
        x = self.fc(x)

        return x

def test(model):
  x = torch.randn(2,3,224,224)
  y = model(x).to(device)

  print(y.shape)
  return y

Resnet18model = Resnet34(ResidualBlock34, layers = [2,2,2,2], num_classes = 10)
test(Resnet18model)

Output:

torch.Size([2, 10])

tensor([[-0.2849, -0.1636, -0.2964, -0.3871, -0.4074, 0.6324, -0.6346, 0.2970, -0.9561, 0.4862], [-0.2434, -0.1617, -0.2317, -0.3054, -0.4313, 0.7819, -0.6532, 0.3620, -0.9633, 0.4460]], device='cuda:0', grad_fn=<ToCopyBackward0>)

Resnet34model = Resnet34(ResidualBlock34,layers = [3,4,6,3], num_classes = 10)
test(Resnet34model)

Output:

torch.Size([2, 10])

tensor([[ 0.1471, 0.2677, 0.2092, -0.5741, -0.0751, 1.0525, -0.1544, -0.1257, 0.5097, 0.8982], [ 0.3452, 0.4786, 0.0690, -0.4927, 0.0151, 0.9735, -0.2605, 0.0686, 0.6679, 1.0258]], device='cuda:0', grad_fn=<ToCopyBackward0>)

Resnet 50 has a different architecture for residual block.

class ResidualBlock50(nn.Module):
  def __init__(self, in_channels:int, out_channels:int, stride:int , downsample = None):
    super().__init__()
    self.conv1 = nn.Sequential(
        #Since the kernel size is 1x1, no spatial information is lost during convolution, and hence, no padding is needed (padding = 0)
        nn.Conv2d(in_channels, out_channels, kernel_size = 1, stride = 1, padding = 0),
        nn.BatchNorm2d(out_channels),
        nn.ReLU()
    )
    self.conv2 = nn.Sequential(
        nn.Conv2d(out_channels, out_channels, kernel_size = 3, stride = stride, padding = 1 ),
        # stride should be 1 here cause input and output shape is same so need to match them
        nn.BatchNorm2d(out_channels),
        nn.ReLU()
    )
    self.conv3 = nn.Sequential(
        nn.Conv2d(out_channels, out_channels * 4 , kernel_size = 1 , stride = 1, padding = 0 ),
        nn.BatchNorm2d(out_channels*4),
        )
    self.relu = nn.ReLU()
    self.downsample = downsample

  def forward(self, x):
    original = x
    x = self.conv1(x)
    x = self.conv2(x)
    x = self.conv3(x)
    if self.downsample: # needed if the original image shape is not same as the output obtained from the conv layers
      original = self.downsample(original)
    x += original
    x = self.relu(x)
    return x
class Resnet50(nn.Module):
  def __init__(self, ResidualBlock50, layers , num_classes):
    super().__init__()
    self.in_channels = 64
    self.conv1 = nn.Sequential(
        nn.Conv2d(3, 64, kernel_size = 7, stride = 2, padding = 3),
        nn.BatchNorm2d(64),
        nn.ReLU()
    )
    self.maxpool = nn.MaxPool2d(kernel_size= 3, stride = 2, padding = 1)
    self.layer0 = self.create_layer(ResidualBlock50 , 64, layers[0], 1)
    self.layer1 = self.create_layer(ResidualBlock50 , 128, layers[1], 2)
    self.layer2 = self.create_layer(ResidualBlock50 , 256, layers[2], 2)
    self.layer3 = self.create_layer(ResidualBlock50 , 512, layers[3], 2)
    self.avgpool = nn.AdaptiveAvgPool2d(output_size=(1,1))
    self.fc = nn.Linear(2048, num_classes)


  def create_layer(self, ResidualBlock50, out_channels, stride, num_blocks):
    downsample = None
    # need to downsample after each residual block even within the layer
    if stride != 1 or self.in_channels != out_channels*4:
      # here the output of one block is 4 times the input, so we need to change the original image channel into 4 times as well , to be able to sum it up.
      downsample = nn.Sequential(
                nn.Conv2d(self.in_channels, out_channels*4, kernel_size=1, stride=stride),
                nn.BatchNorm2d(out_channels*4),
          )
    all_blocks = []

    all_blocks.append(ResidualBlock50(self.in_channels, out_channels, stride , downsample))
    self.in_channels = out_channels*4

    for i in range(num_blocks - 1 ):
      all_blocks.append(ResidualBlock50(self.in_channels, out_channels, 1, downsample = None))

    return nn.Sequential(*all_blocks)


  def forward(self, x):
    x = self.conv1(x)
    x = self.maxpool(x)
    x = self.layer0(x)
    x = self.layer1(x)
    x = self.layer2(x)
    x = self.layer3(x)
    x = self.avgpool(x)
    x = torch.flatten(x, 1)
    x = self.fc(x)

    return x

Resnet50model = Resnet50(ResidualBlock50, layers = [3,4,6,3], num_classes = 10)
test(Resnet50model)
# to create Resnet 101 and 152, just change the layers list

Output:
torch.Size([2, 10])

tensor([[-0.3004, -0.0101, -0.8938, 1.1565, 0.1256, -1.1083, 1.0718, 0.9870, 1.0931, 0.3080], [-0.9998, 0.1942, 1.0766, 0.0599, 0.2273, -0.3382, 0.9440, 0.2865, -0.0568, -0.2057]], device='cuda:0', grad_fn=<ToCopyBackward0>)

Resnet101model = Resnet50(ResidualBlock50, layers = [3,4,23,3], num_classes = 10)
Resnet152model = Resnet50(ResidualBlock50, layers = [3,8,36,3], num_classes = 10)

test(Resnet101model)

Output:

torch.Size([2, 10])

tensor([[ 1.0657, 0.4926, -0.4928, -0.8665, -0.7191, 0.2572, 0.9884, 0.5090, -0.3708, 0.9221], [ 0.5310, 1.3553, 0.0656, 0.4143, -0.9829, 0.1307, -0.2942, 0.4128, -0.9420, -0.5224]], device='cuda:0', grad_fn=<ToCopyBackward0>)

test(Resnet152model)

Output:

torch.Size([2, 10])

tensor([[ 0.9582, 0.3727, 0.4013, -0.1902, -0.1416, 0.3467, 0.0930, -1.0278, -0.3439, -0.0607], [-0.4680, 1.5141, 0.2227, -0.9539, 1.0604, 0.8895, 0.5435, -0.1507, 0.6274, 0.4414]], device='cuda:0', grad_fn=<ToCopyBackward0>)