Everything about Unet

U-Net : CNNs for Biomedical Image Segmentation

Jun 13, 2024 7 min read

Unet

Paper Walkthrough

1. Abstract

The proposed network, called U-Net, has two main parts: one part captures the overall context of the image, and the other part ensures precise localization of features. This design helps the network perform well even with limited data.

The U-Net outperforms previous methods for segmenting neuronal structures in electron microscope images. It also won a cell tracking competition with a large margin when trained on transmitted light microscopy images.

Basically, they provided a training strategy that uses data augmentation techniques such that we can achieve high accuracy very quick even with less amount of data.
It consists of a contraction path to capture details i.e. it tells “what” and a symmetric expanding path that enables precise localization i.e. it tells “where”.

2. Introduction

U-Net is a type of convolutional network designed for biomedical image segmentation. Traditional convolutional networks were not very successful in this field due to the limited size of training datasets and the need for precise localization of features in images.

Simply saying, mostly CNN were used in classification tasks, but in most biomedical image processing , we need to have localization( should tell/detect where an object is i.e. output label is supposed to be assigned to each pixel) and also not much training data is available for such biomedical tasks. Previous works used Sliding window approach for object detection and localization which is very slow and low accuracy whilst being resource intensive.

U-Net overcomes these issues with a U-shaped architecture that consists of a contracting path to capture context and an expanding path to achieve precise localization. This design allows U-Net to work well even with a small amount of training data.

Key features of U-Net include:

Contracting Path: Captures the context of the image.
Expanding Path: Ensures precise localization.
Data Augmentation: Uses techniques like elastic deformations to make the most of limited training data.
Overlap-Tile Strategy: Allows seamless segmentation of large images by mirroring the input image for missing data.

U-Net has been highly successful in various biomedical segmentation tasks, winning competitions and outperforming previous methods.

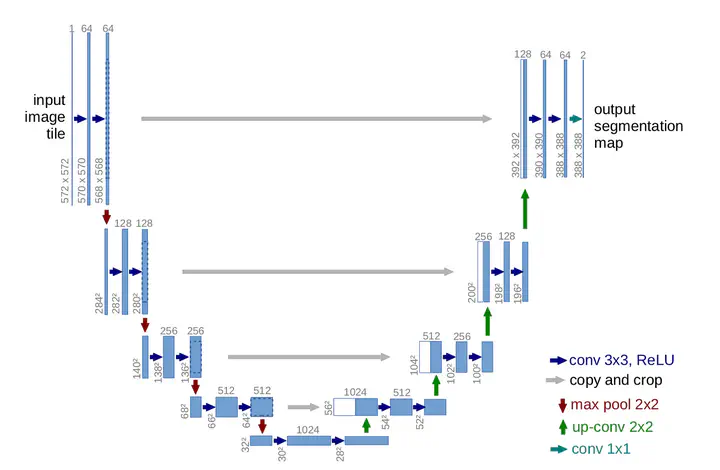
3. Network Architecture

The U-Net architecture consists of two main parts: the contracting path and the expansive path.

Contracting Path (Left Side):
- This part follows a typical convolutional network structure.
- Repeated application of two 3x3 convolutions (without padding), each followed by a ReLU activation.
- Downsampling is done using a 2x2 max pooling operation with stride 2.
- The number of feature channels doubles at each downsampling step.
Expansive Path (Right Side):
- This part involves upsampling the feature map followed by a 2x2 convolution (up-convolution), which halves the number of feature channels.
- The upsampled feature map is concatenated with the correspondingly cropped feature map from the contracting path.
- Followed by two 3x3 convolutions, each followed by a ReLU.
- Cropping is necessary due to the loss of border pixels in every convolution.
Final Layer:
- A 1x1 convolution is used to map each 64-component feature vector to the desired number of classes.
Overall Structure:
- The network has a total of 23 convolutional layers.
- Input tile size is selected to ensure that all 2x2 max-pooling operations are applied to layers with even x- and y-dimensions, allowing seamless tiling of the output segmentation map.

4. Conclusion

The U-Net architecture demonstrates excellent performance across various biomedical segmentation applications. Its effectiveness is largely due to the use of data augmentation with elastic deformations, allowing it to achieve high accuracy with a minimal number of annotated images. Training time is also efficient, taking only 10 hours on an NVidia Titan GPU (6 GB). The full implementation based on Caffe and the trained networks are available for use. We are confident that the U-Net architecture can be easily adapted to a wide range of other tasks.

Code Implementation

import torch  # PyTorch library for deep learning
import torch.nn as nn  # PyTorch module for neural network layers
import torchvision  # PyTorch library for vision-related tasks
from torchvision.transforms import v2  # Importing version 2 of transforms from torchvision

# Define a basic convolutional block
class Block(nn.Module):
    def __init__(self, in_ch, out_ch):
        super().__init__()
        self.conv1 = nn.Conv2d(in_ch, out_ch, 3)  # First 3x3 convolution
        self.relu  = nn.ReLU()  # ReLU activation function
        self.conv2 = nn.Conv2d(out_ch, out_ch, 3)  # Second 3x3 convolution

    def forward(self, x):
        return self.conv2(self.relu(self.conv1(x)))  # Apply conv1, ReLU, then conv2

# Define the encoder part of the U-Net
class Encoder(nn.Module):
    def __init__(self, chs=(1,64,128,256,512,1024)):
        super().__init__()
        # Create a list of convolutional blocks for the encoder
        self.enc_blocks = nn.ModuleList([Block(chs[i], chs[i+1]) for i in range(len(chs)-1)])
        self.pool       = nn.MaxPool2d(2)  # Max pooling layer with 2x2 window

    def forward(self, x):
        encoder_ftrs = []  # List to store features from each block
        for block in self.enc_blocks:
            x = block(x)  # Apply block
            encoder_ftrs.append(x)  # Store the features
            x = self.pool(x)  # Downsample using max pooling
        return encoder_ftrs  # Return the list of features

# Instantiate and test the encoder
encoder = Encoder()
y = encoder(torch.randn(1,1,572,572))  # Create a random tensor and pass it through the encoder
for i in y:
  print(i.shape)  # Print the shape of each feature map

# Define the decoder part of the U-Net
class Decoder(nn.Module):
    def __init__(self, chs=(1024, 512, 256, 128, 64)):
        super().__init__()
        self.chs = chs
        # Create a list of up-convolutions for the decoder
        self.upconvs = nn.ModuleList([nn.ConvTranspose2d(chs[i], chs[i+1], 2, 2) for i in range(len(chs)-1)])
        # Create a list of convolutional blocks for the decoder
        self.dec_blocks = nn.ModuleList([Block(chs[i], chs[i+1]) for i in range(len(chs)-1)])

    def forward(self, x, encoder_features):
        for i in range(len(self.chs)-1):
            x = self.upconvs[i](x)  # Apply up-convolution
            enc_ftrs = self.crop(encoder_features[i], x)  # Crop encoder features to match size
            x = torch.cat([x, enc_ftrs], dim=1)  # Concatenate along the channel dimension
            x = self.dec_blocks[i](x)  # Apply block
        return x

    def crop(self, enc_ftrs, x):
        _, _, H, W = x.shape  # Get height and width of the current feature map
        enc_ftrs = v2.CenterCrop([H, W])(enc_ftrs)  # Crop encoder features to match size
        return enc_ftrs

# Define the complete U-Net architecture
class UNet(nn.Module):
    def __init__(self, enc_chs=(1,64,128,256,512,1024), dec_chs=(1024, 512, 256, 128, 64), num_class=2, retain_dim=False, out_sz=(572,572)):
        super().__init__()
        self.encoder = Encoder(enc_chs)  # Encoder part
        self.decoder = Decoder(dec_chs)  # Decoder part
        self.head = nn.Conv2d(dec_chs[-1], num_class, 1)  # Final 1x1 convolution to get the desired number of classes
        self.retain_dim = retain_dim  # Flag to retain input dimensions
        self.out_sz = out_sz  # Output size for resizing
        self.dec_chs = dec_chs

    def forward(self, x):
        enc_ftrs = self.encoder(x)  # Pass input through the encoder
        x = self.decoder(enc_ftrs[::-1][0], enc_ftrs[::-1][1:])  # Pass through the decoder
        x = self.head(x)  # Apply final 1x1 convolution

        if self.retain_dim:
            x = F.interpolate(x, self.out_sz)  # Resize to original size if needed
        return x

# Function to test the U-Net
device = "cuda" if torch.cuda.is_available() else "cpu"  # Use GPU if available
def test():
    x = torch.randn((1,1,572,572))  # Create a random input tensor
    unet = UNet()  # Instantiate U-Net
    y = unet(x).to(device)  # Pass the input through the network and move to device
    print(y.shape)  # Print the shape of the output
    return y

test()  # Call the test function

**Output:** 

torch.Size([1, 2, 388, 388])

tensor([[[[0.1185, 0.1221, 0.1037, ..., 0.1453, 0.1324, 0.1648], [0.1233, 0.1126, 0.1103, ..., 0.1208, 0.1409, 0.1587], [0.1214, 0.1028, 0.1219, ..., 0.1013, 0.1268, 0.1299], ..., [0.1024, 0.1200, 0.1477, ..., 0.1080, 0.1503, 0.1457], [0.1202, 0.1244, 0.1539, ..., 0.1167, 0.1352, 0.0953], [0.1027, 0.1163, 0.1189, ..., 0.1374, 0.1486, 0.1419]], [[0.0748, 0.1326, 0.0768, ..., 0.1243, 0.1086, 0.0762], [0.0989, 0.0993, 0.0903, ..., 0.1428, 0.0943, 0.0931], [0.1668, 0.1122, 0.0907, ..., 0.1454, 0.0823, 0.1306], ..., [0.1078, 0.0896, 0.1040, ..., 0.0974, 0.1020, 0.1220], [0.1109, 0.1060, 0.0724, ..., 0.0976, 0.1141, 0.1312], [0.1201, 0.0795, 0.1041, ..., 0.0782, 0.1263, 0.1219]]]], grad_fn=<ConvolutionBackward0>)

works good!

Retain_dim = true changes the size of output to the input size using bilinear interpolation(taking average of neighboring pixels to fill in new spots to enlarge the image)
Why even bother resizing the output image using retain_dim ? cause it is easier to calculate the loss if the output image and input image both are of same dimensions.